Calculate the total O:E ratio — oecalc • metamisc

This function calculates (transformed versions of) the ratio of total number of observed versus expected events with the corresponding sampling variance.

Usage

oecalc(
  OE,
  OE.se,
  OE.cilb,
  OE.ciub,
  OE.cilv,
  EO,
  EO.se,
  citl,
  citl.se,
  N,
  O,
  E,
  Po,
  Po.se,
  Pe,
  data,
  slab,
  add = 1/2,
  g = NULL,
  level = 0.95,
  ...
)

Arguments

OE: vector with the estimated ratio of total observed versus total expected events
OE.se: Optional vector with the standard errors of the estimated O:E ratios.
OE.cilb: Optional vector to specify the lower limits of the confidence interval for OE.
OE.ciub: Optional vector to specify the upper limits of the confidence interval for OE.
OE.cilv: Optional vector to specify the levels of aformentioned confidence interval limits. (default: 0.95, which corresponds to the 95% confidence interval).
EO: Optional vector with the estimated ratio of total expected versus total observed events
EO.se: Optional vector with the standard errors of the estimated E:O ratios
citl: Optional vector with the estimated calibration-in-the-large statistics
citl.se: Optional vector with the standard error of the calibration-in-the-large statistics
N: Optional vector to specify the sample/group sizes.
O: Optional vector to specify the total number of observed events.
E: Optional vector to specify the total number of expected events
Po: Optional vector to specify the (cumulative) observed event probabilities.
Po.se: Optional vector with the standard errors of Po. For time-to-event data, these could also be the SE of the observed survival probabilities (e.g. as obtained from Kaplan-Meier analysis)
Pe: Optional vector to specify the (cumulative) expected event probabilites (if specified, during time t.val)
data: Optional data frame containing the variables given to the arguments above.
slab: Optional vector with labels for the studies.
add: a non-negative number indicating the amount to add to zero counts. See `Details'
g: a quoted string that is the function to transform estimates of the total O:E ratio; see the details below.
level: level for confidence interval, default 0.95.
...: Additional arguments.

Value

An object of class c("mm_perf","data.frame") with the following columns:

"theta": The (transformed) O:E ratio.
"theta.se": Standard errors of the (transformed) O:E ratio.
"theta.cilb": Lower confidence interval of the (transformed) O:E ratios. The level is specified in level. Intervals are calculated on the same scale as theta by assuming a Normal distribution.
"theta.ciub": Upper confidence interval of the (transformed) c-statistics. The level is specified in level. Intervals are calculated on the same scale as theta by assuming a Normal distribution.
"theta.source": Method used for calculating the (transformed) O:E ratio.
"theta.se.source": Method used for calculating the standard error of the (transformed) O:E ratio.

References

Debray TPA, Damen JAAG, Snell KIE, Ensor J, Hooft L, Reitsma JB, et al. A guide to systematic review and meta-analysis of prediction model performance. BMJ. 2017;356:i6460.

Debray TPA, Damen JAAG, Riley R, Snell KIE, Reitsma JB, Hooft L, et al. A framework for meta-analysis of prediction model studies with binary and time-to-event outcomes. Stat Methods Med Res. 2019 Sep;28(9):2768--86.

Snell KI, Ensor J, Debray TP, Moons KG, Riley RD. Meta-analysis of prediction model performance across multiple studies: Which scale helps ensure between-study normality for the C -statistic and calibration measures? Stat Methods Med Res. 2017.

Author

Thomas Debray <thomas.debray@gmail.com>

Examples

######### Validation of prediction models with a binary outcome #########
data(EuroSCORE)

# Calculate the total O:E ratio and its standard error
est1 <- oecalc(O = n.events, E = e.events, N = n, data = EuroSCORE, slab = Study)
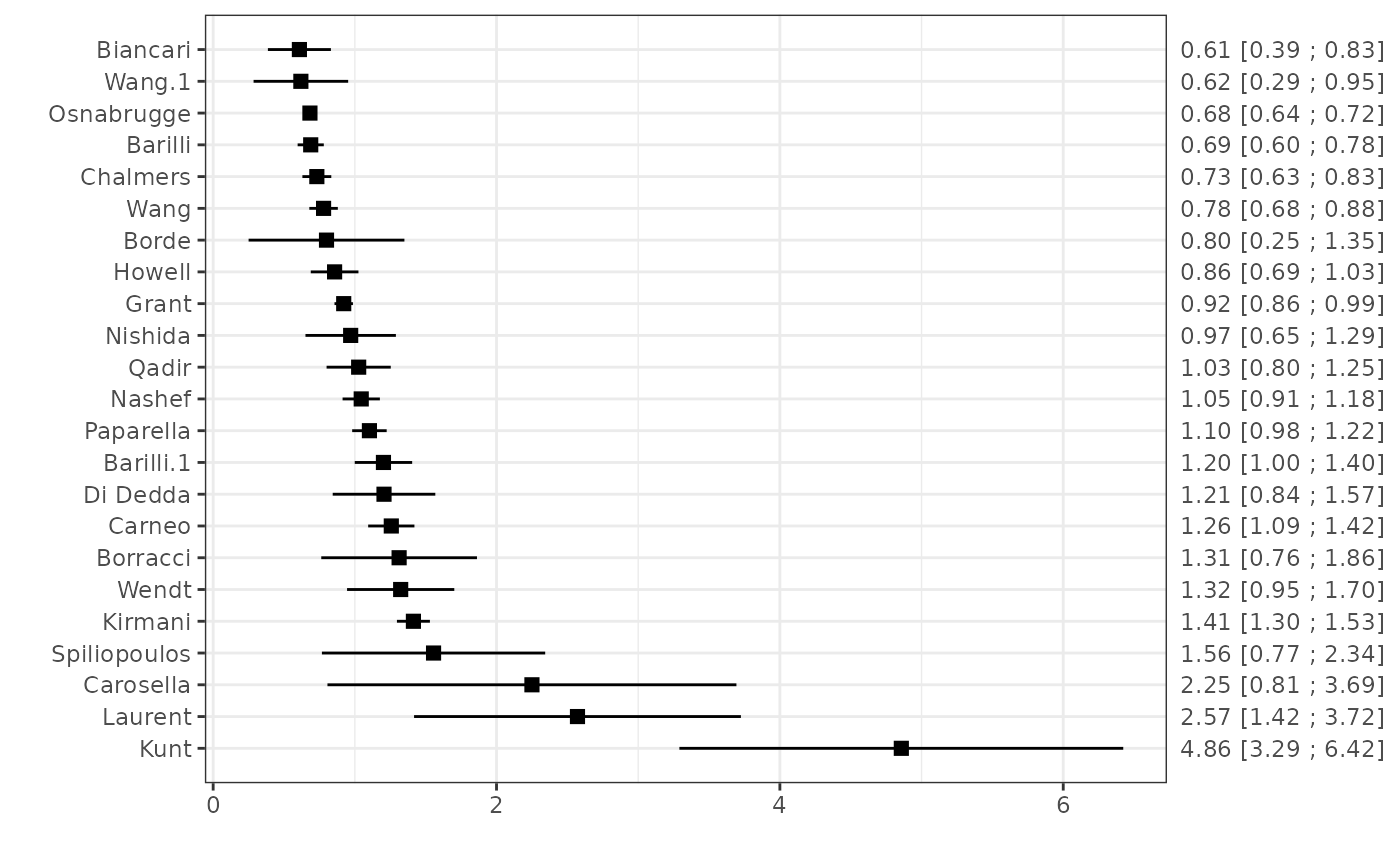
est1
#>                  theta   theta.se theta.cilb theta.ciub theta.source    O
#> Nashef       1.0450450 0.06716203  0.9134099  1.1766802   O, E and N  232
#> Biancari     0.6086957 0.11345371  0.3863305  0.8310608   O, E and N   28
#> Di Dedda     1.2058824 0.18475130  0.8437765  1.5679882   O, E and N   41
#> Chalmers     0.7318008 0.05203645  0.6298112  0.8337903   O, E and N  191
#> Grant        0.9214541 0.03320253  0.8563783  0.9865298   O, E and N  746
#> Carneo       1.2573099 0.08328543  1.0940735  1.4205464   O, E and N  215
#> Kunt         4.8571429 0.79922240  3.2906957  6.4235900   O, E and N   34
#> Kirmani      1.4134367 0.05935803  1.2970971  1.5297763   O, E and N  547
#> Howell       0.8571429 0.08588255  0.6888162  1.0254696   O, E and N   90
#> Wang         0.7793103 0.05131185  0.6787410  0.8798797   O, E and N  226
#> Borde        0.8000000 0.28056169  0.2501092  1.3498908   O, E and N    8
#> Qadir        1.0270270 0.11555260  0.8005481  1.2535060   O, E and N   76
#> Spiliopoulos 1.5555556 0.40204098  0.7675697  2.3435414   O, E and N   14
#> Wendt        1.3235294 0.19309081  0.9450784  1.7019804   O, E and N   45
#> Laurent      2.5714286 0.58846311  1.4180621  3.7247951   O, E and N   18
#> Wang.1       0.6190476 0.17032315  0.2852204  0.9528749   O, E and N   13
#> Nishida      0.9705882 0.16279815  0.6515097  1.2896668   O, E and N   33
#> Barilli      0.6885246 0.04710205  0.5962063  0.7808429   O, E and N  210
#> Barilli.1    1.2019231 0.10340170  0.9992595  1.4045867   O, E and N  125
#> Paparella    1.1029412 0.06211634  0.9811954  1.2246870   O, E and N  300
#> Carosella    2.2500000 0.73637626  0.8067290  3.6932710   O, E and N    9
#> Borracci     1.3125000 0.28036848  0.7629879  1.8620121   O, E and N   21
#> Osnabrugge   0.6830357 0.02064915  0.6425641  0.7235073   O, E and N 1071
#>                    E     N
#> Nashef        222.00  5553
#> Biancari       46.00  1027
#> Di Dedda       34.00  1090
#> Chalmers      261.00  5576
#> Grant         809.59 23740
#> Carneo        171.00  3798
#> Kunt            7.00   428
#> Kirmani       387.00 15497
#> Howell        105.00   933
#> Wang          290.00 11170
#> Borde          10.00   498
#> Qadir          74.00  2004
#> Spiliopoulos    9.00   216
#> Wendt          34.00  1066
#> Laurent         7.00   314
#> Wang.1         21.00   818
#> Nishida        34.00   461
#> Barilli       305.00 12201
#> Barilli.1     104.00  1670
#> Paparella     272.00  6191
#> Carosella       4.00   250
#> Borracci       16.00   503
#> Osnabrugge   1568.00 50588

# Calculate the log of the total O:E ratio and its standard error
est2 <- oecalc(O = n.events, E = e.events, N = n, data = EuroSCORE, slab = Study, g = "log(OE)")
est2
#>                    theta   theta.se   theta.cilb  theta.ciub theta.source    O
#> Nashef        0.04405999 0.06426711 -0.081901240  0.17002122   O, E and N  232
#> Biancari     -0.49643689 0.18638824 -0.861751123 -0.13112265   O, E and N   28
#> Di Dedda      0.18721154 0.15320840 -0.113071397  0.48749448   O, E and N   41
#> Chalmers     -0.31224698 0.07110740 -0.451614919 -0.17287904   O, E and N  191
#> Grant        -0.08180235 0.03603276 -0.152425252 -0.01117944   O, E and N  746
#> Carneo        0.22897447 0.06624097  0.099144553  0.35880439   O, E and N  215
#> Kunt          1.58045038 0.16454579  1.257946559  1.90295419   O, E and N   34
#> Kirmani       0.34602411 0.04199553  0.263714374  0.42833385   O, E and N  547
#> Howell       -0.15415068 0.10019631 -0.350531831  0.04223047   O, E and N   90
#> Wang         -0.24934592 0.06584264 -0.378395127 -0.12029672   O, E and N  226
#> Borde        -0.22314355 0.35070211 -0.910507050  0.46421995   O, E and N    8
#> Qadir         0.02666825 0.11251174 -0.193850721  0.24718721   O, E and N   76
#> Spiliopoulos  0.44183275 0.25845491 -0.064729568  0.94839507   O, E and N   14
#> Wendt         0.28030197 0.14589084 -0.005638818  0.56624275   O, E and N   45
#> Laurent       0.94446161 0.22884677  0.495930190  1.39299303   O, E and N   18
#> Wang.1       -0.47957308 0.27513739 -1.018832454  0.05968629   O, E and N   13
#> Nishida      -0.02985296 0.16773143 -0.358600527  0.29889460   O, E and N   33
#> Barilli      -0.37320425 0.06841012 -0.507285614 -0.23912288   O, E and N  210
#> Barilli.1     0.18392284 0.08603021  0.015306718  0.35253896   O, E and N  125
#> Paparella     0.09798041 0.05631881 -0.012402434  0.20836325   O, E and N  300
#> Carosella     0.81093022 0.32727834  0.169476459  1.45238397   O, E and N    9
#> Borracci      0.27193372 0.21361408 -0.146742192  0.69060962   O, E and N   21
#> Osnabrugge   -0.38120813 0.03023143 -0.440460642 -0.32195562   O, E and N 1071
#>                    E     N
#> Nashef        222.00  5553
#> Biancari       46.00  1027
#> Di Dedda       34.00  1090
#> Chalmers      261.00  5576
#> Grant         809.59 23740
#> Carneo        171.00  3798
#> Kunt            7.00   428
#> Kirmani       387.00 15497
#> Howell        105.00   933
#> Wang          290.00 11170
#> Borde          10.00   498
#> Qadir          74.00  2004
#> Spiliopoulos    9.00   216
#> Wendt          34.00  1066
#> Laurent         7.00   314
#> Wang.1         21.00   818
#> Nishida        34.00   461
#> Barilli       305.00 12201
#> Barilli.1     104.00  1670
#> Paparella     272.00  6191
#> Carosella       4.00   250
#> Borracci       16.00   503
#> Osnabrugge   1568.00 50588

# Display the results of all studies in a forest plot
plot(est1)