Imputation via Joint Modelling
Imputation via Joint Modelling

Imputation via Joint Modelling
It is common to assume that all data follow a multivariate Normal or Student-T distribution
\((𝑥_1,𝑥_2,𝑦) \sim MVN (𝜇,"Σ" )\)
For now, we consider that
- The mean vector μ is known
- The covariance matrix Σ is known
Imputation via Joint Modelling

Imputation via Joint Modelling
How to use the conditional mean?
\(𝜇_1^∗\) is the most likely value for \(𝑥_1\), and can thus be used as imputation.
\(𝜇_1^∗\) is equal to the mean of \(𝑥_1\) plus an adjustment.
- If there is little correlation between the predictors and outcomes, then the best guess for \(𝑥_1\) is the mean of \(𝑥_1\).
Imputation via Joint Modelling
Example
Multivariate distribution of patients presenting with lower respiratory tract infections in primary care:
- Age, years: mean = 52, SD = 16
- C-reactive protein: mean = 53, SD = 62
- Temperature, C°: mean = 37.5, SD = 0.8
- Cor (Age, CRP) = 0.09
- Cor(Age, Temperature) = -0.15
- Cor(CRP, Temperature) = 0.25
Imputation via Joint Modelling

Imputation via Joint Modelling
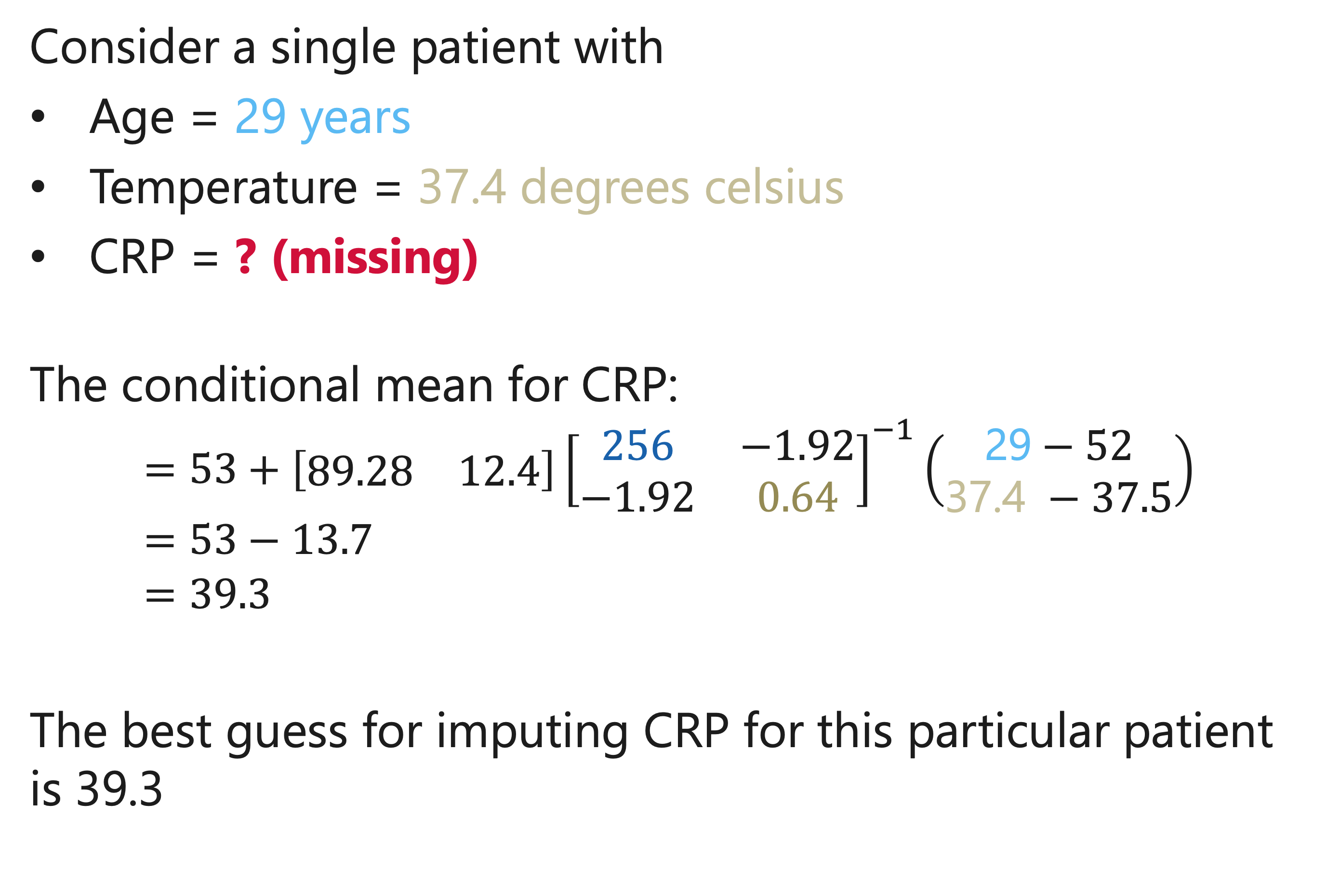
Imputation via Joint Modelling

Imputation via Joint Modelling
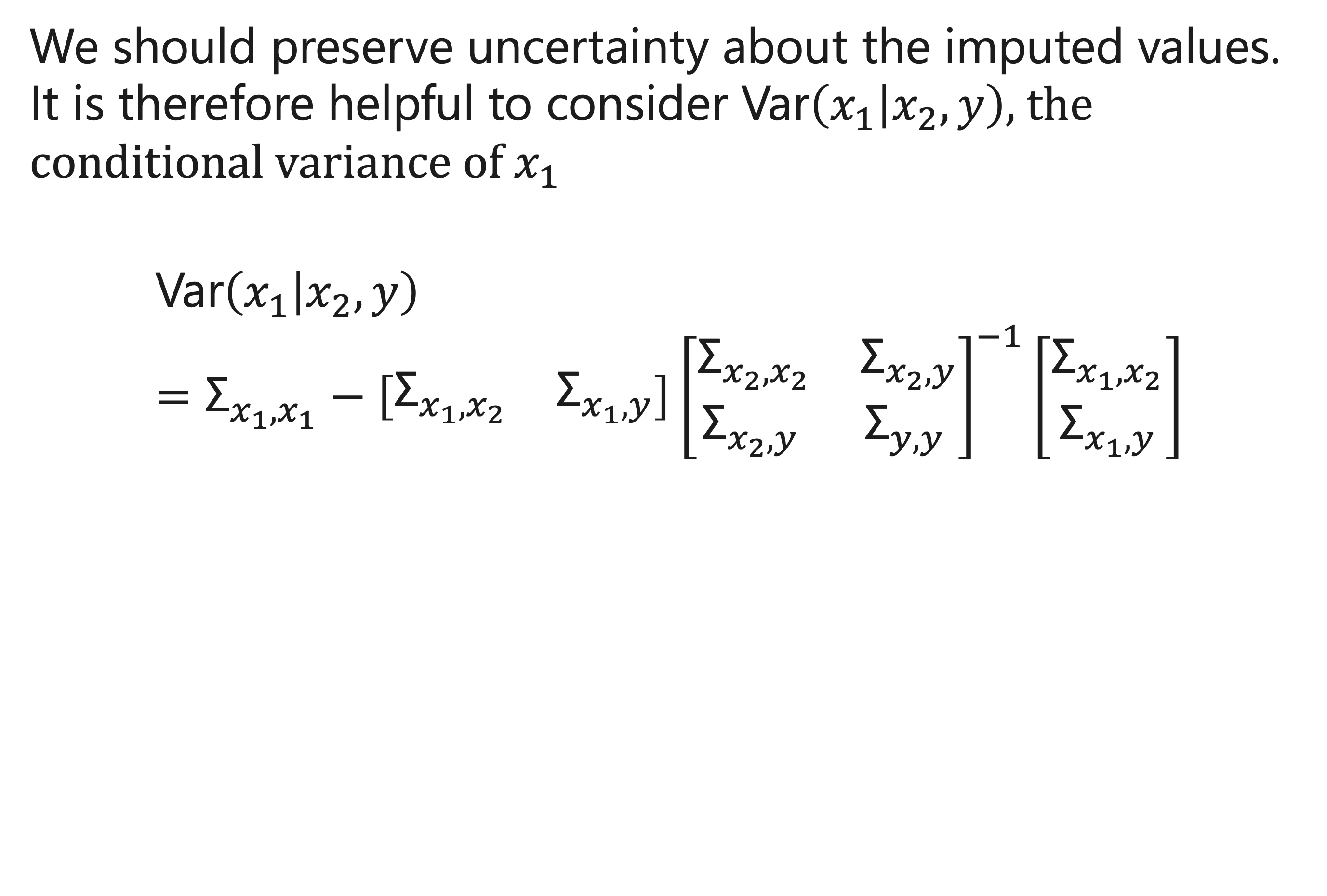
Imputation via Joint Modelling
How to use the conditional variance?
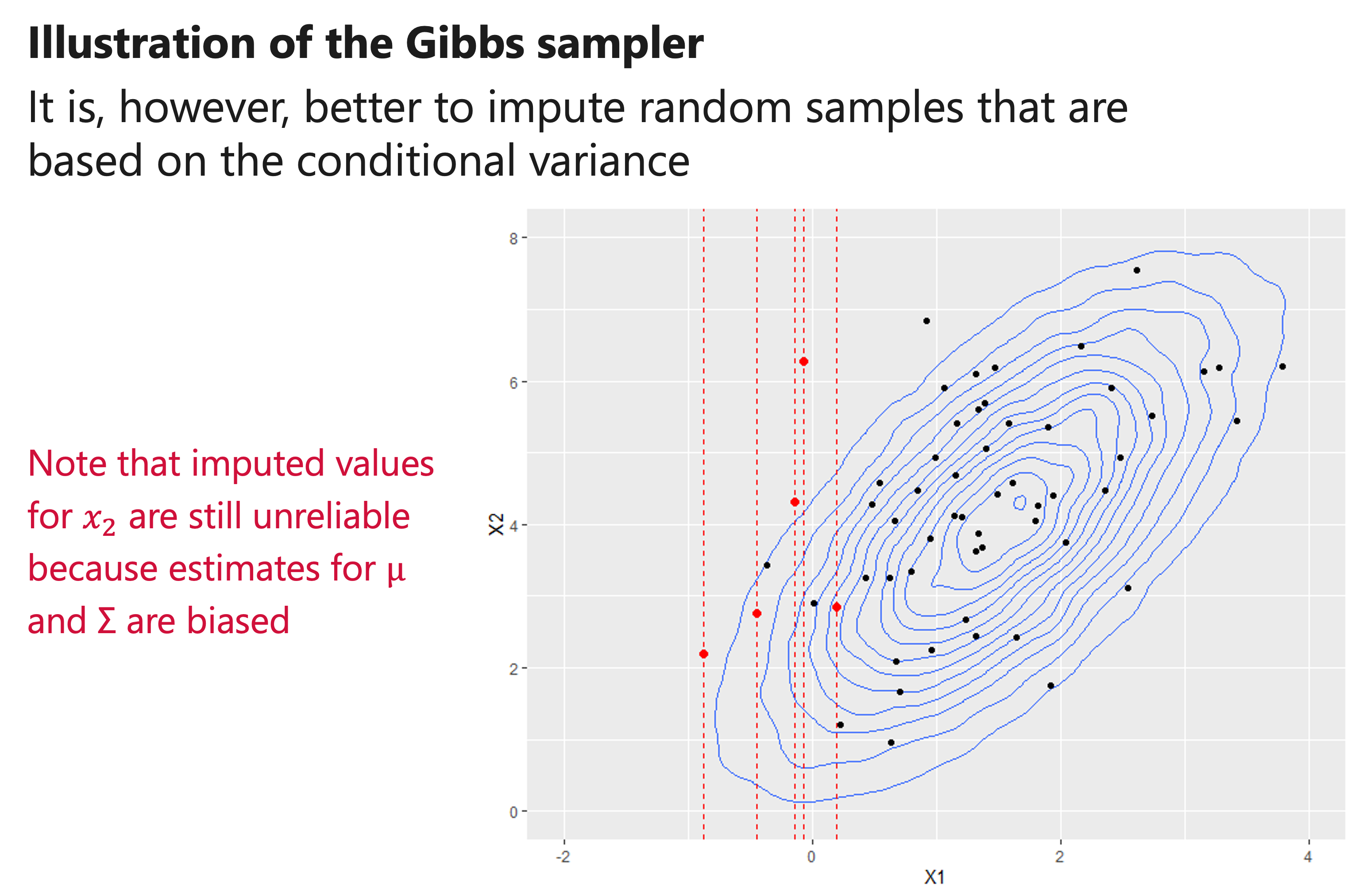
“Var” \((𝑥_1│𝑥_2, 𝑦)\) quantifies the variance of \(𝜇_1^∗\) , and can be used to draw multiple imputations. In particular, we can sample an imputed value from a Normal distribution with mean \(𝜇_1^∗\) and variance “Var” \((𝑥_1│𝑥_2, 𝑦)\)
“Var” \((𝑥_1│𝑥_2, 𝑦)\) is equal to the variance of \(𝑥_1\) minus an adjustment. If there is little correlation between the predictors and outcomes, then the variance of imputed values for \(𝑥_1\) is equal to the variance of \(𝑥_1\) in the original population.
Imputation via Joint Modelling

Imputation via Joint Modelling

Imputation via Joint Modelling
So, how to generate an imputed dataset?
An iterative procedure is needed:
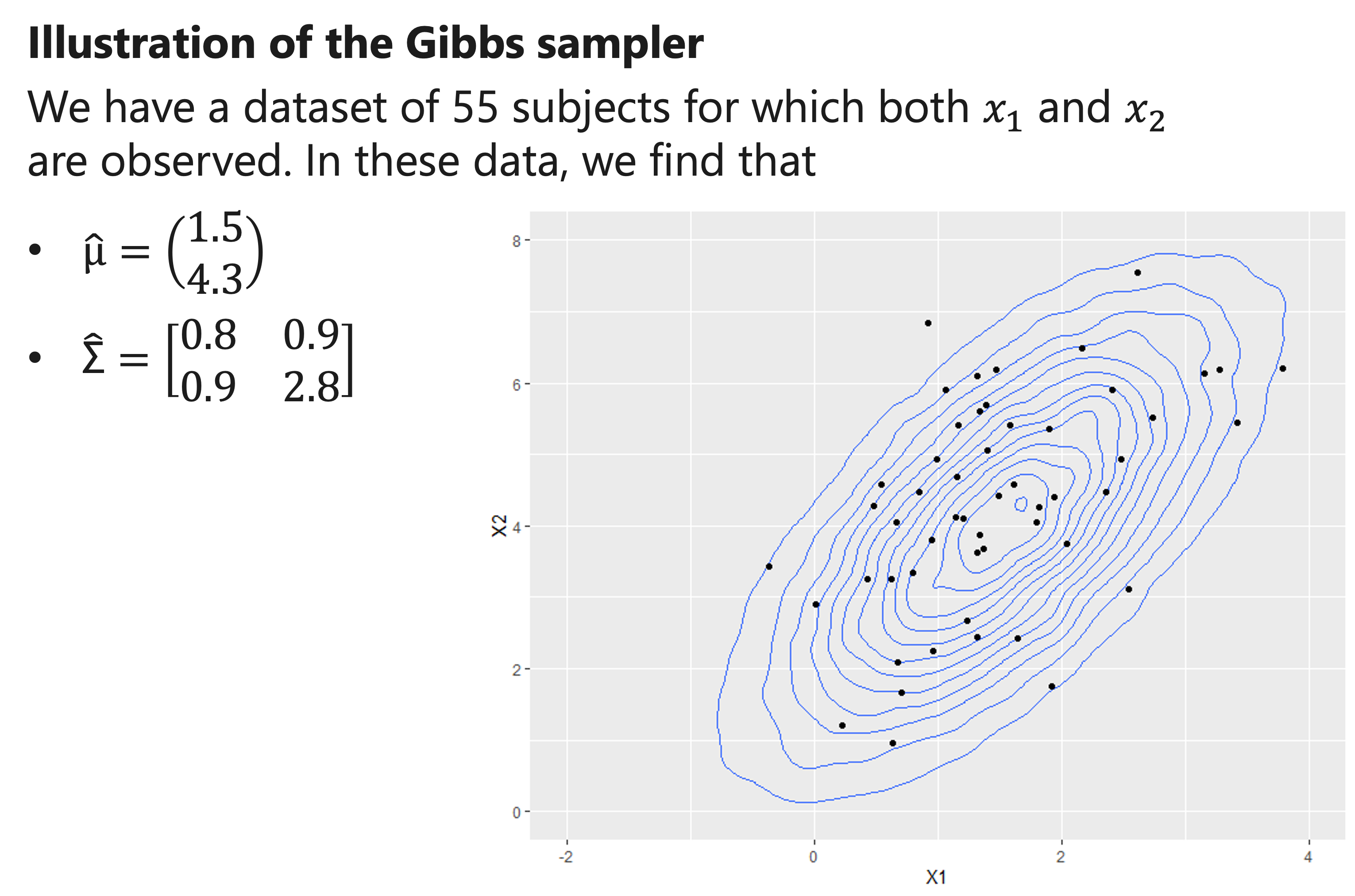
- Estimate μ and Σ
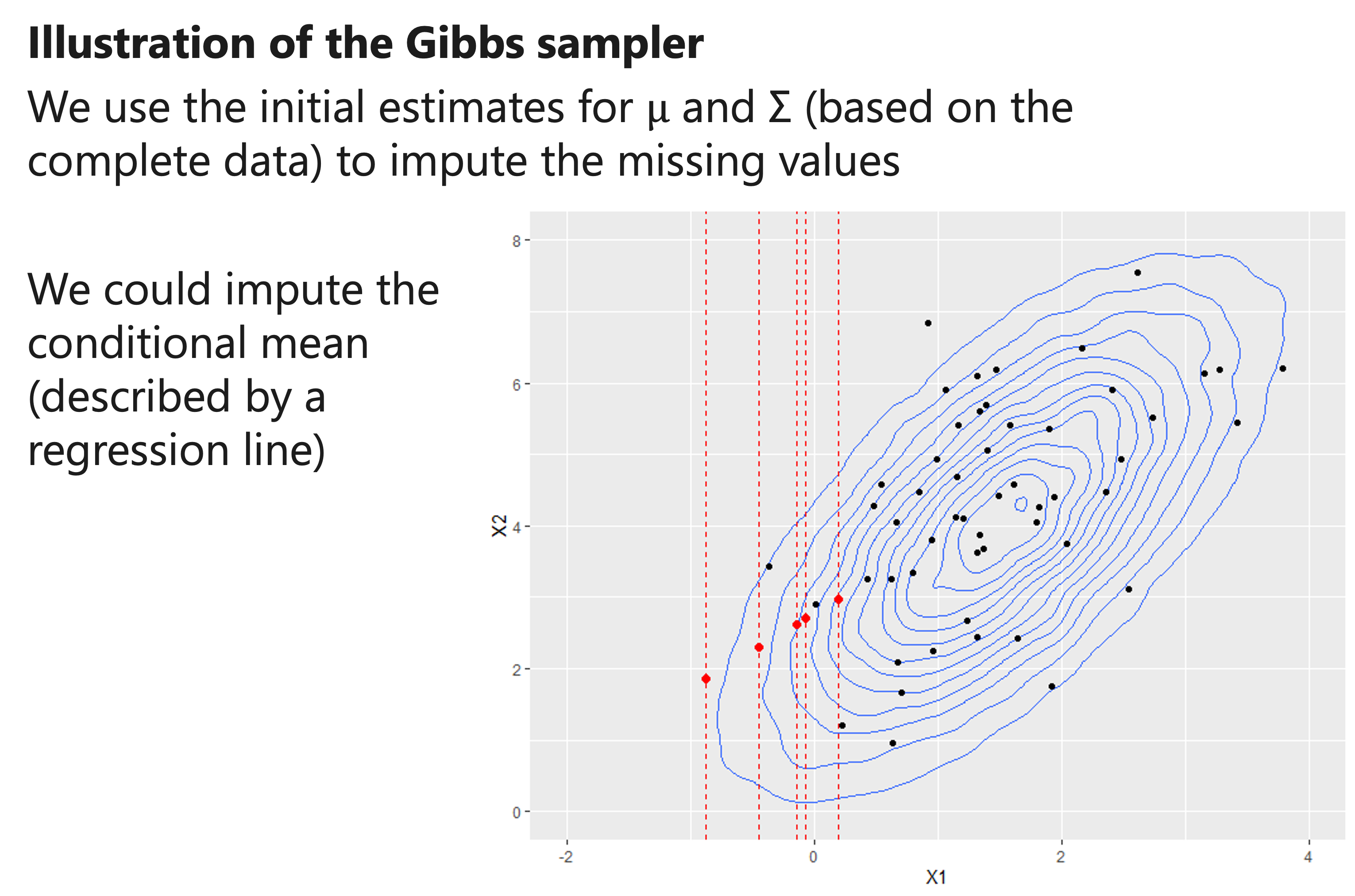
- Use μ and Σ to impute the missing values
- Update estimates of μ and Σ using the imputed values
- Continue until estimates of μ and Σ stabilize
This approach is known as the Gibbs sampler
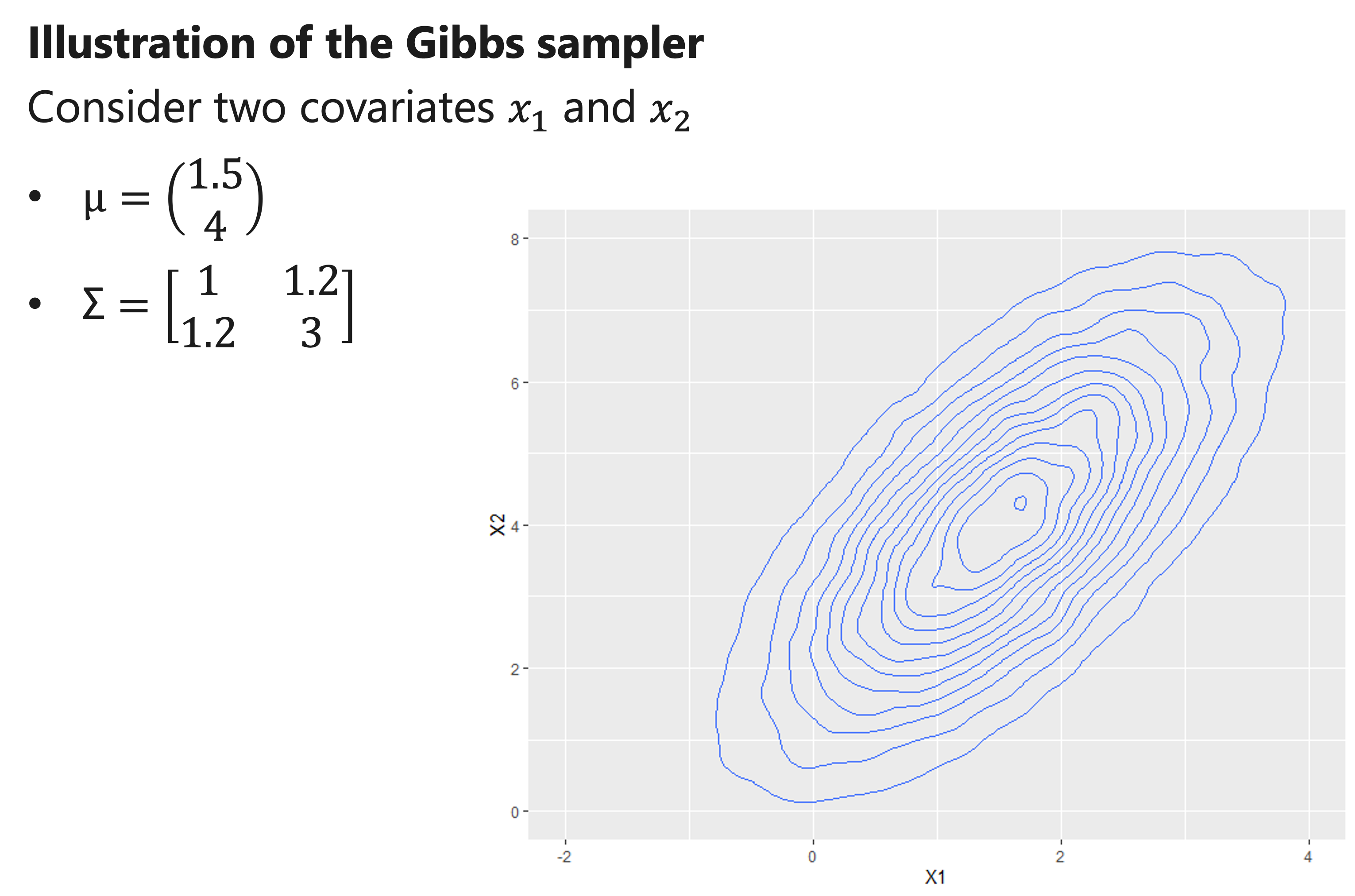
A natural choice for the initial estimates of μ and Σ is to derive them directly using the complete data only.
Imputation via Joint Modelling
Imputation via Joint Modelling
Imputation via Joint Modelling
Imputation via Joint Modelling
Imputation via Joint Modelling
Imputation via Joint Modelling
Imputation via Joint Modelling
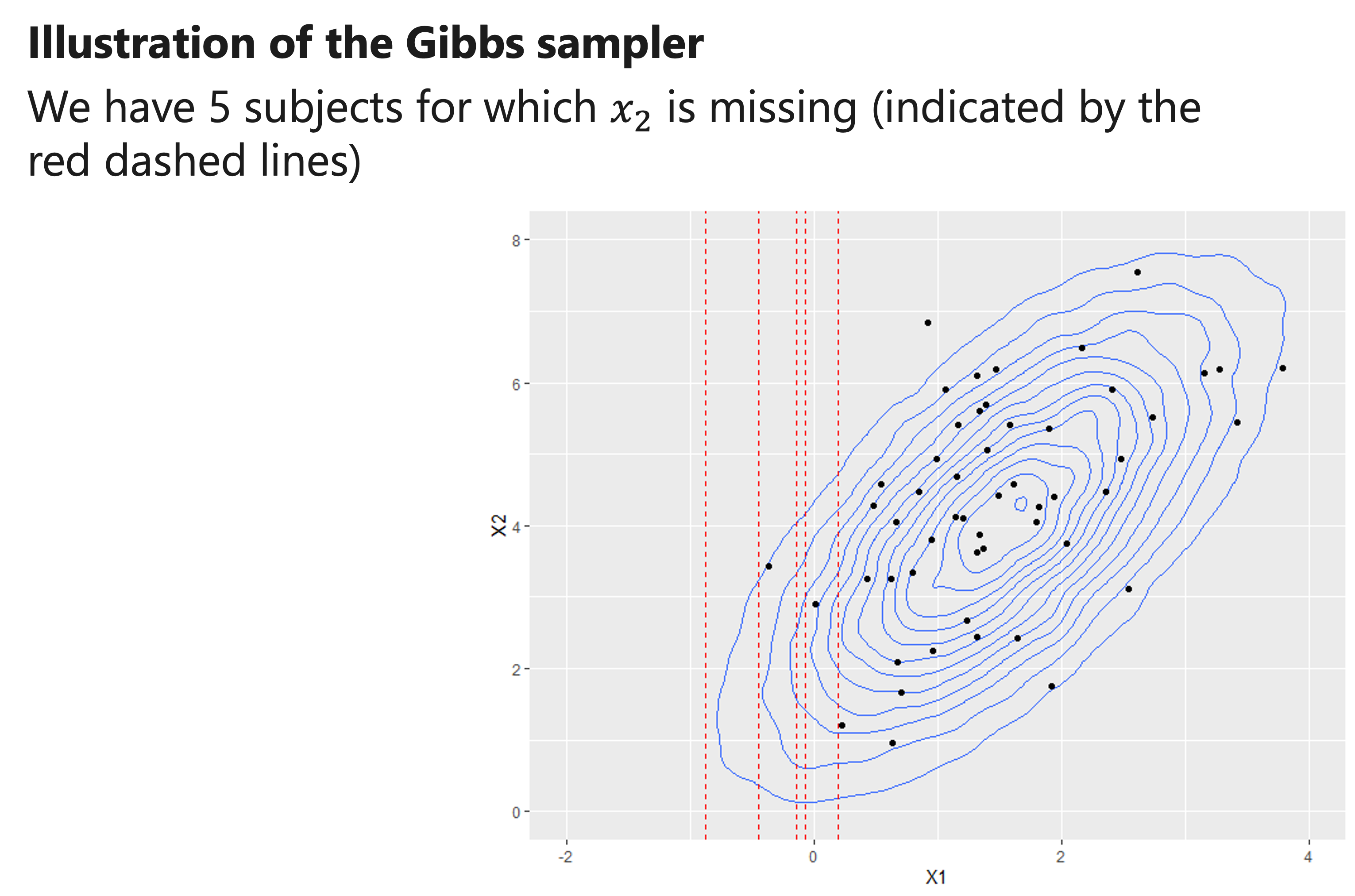
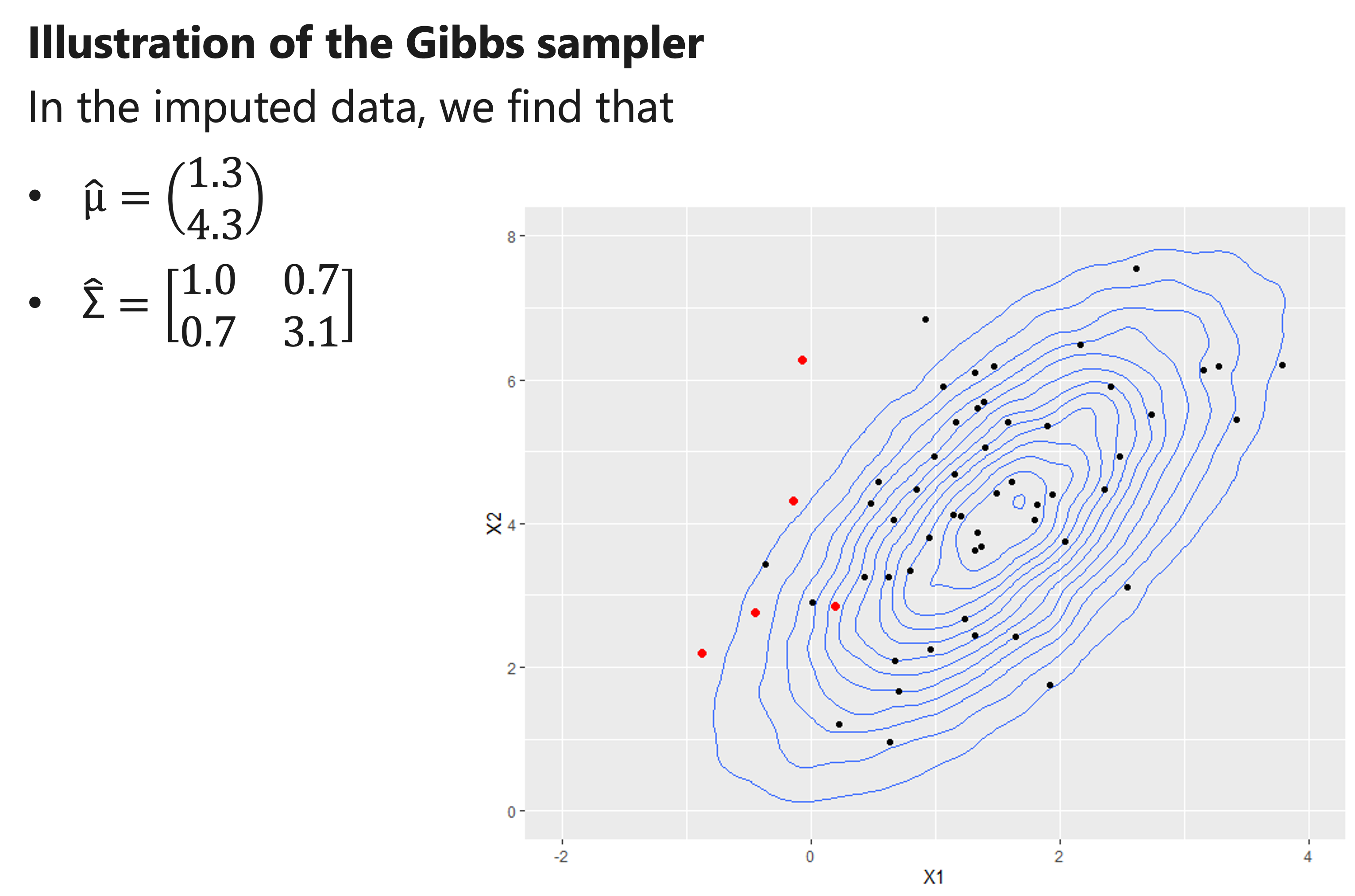
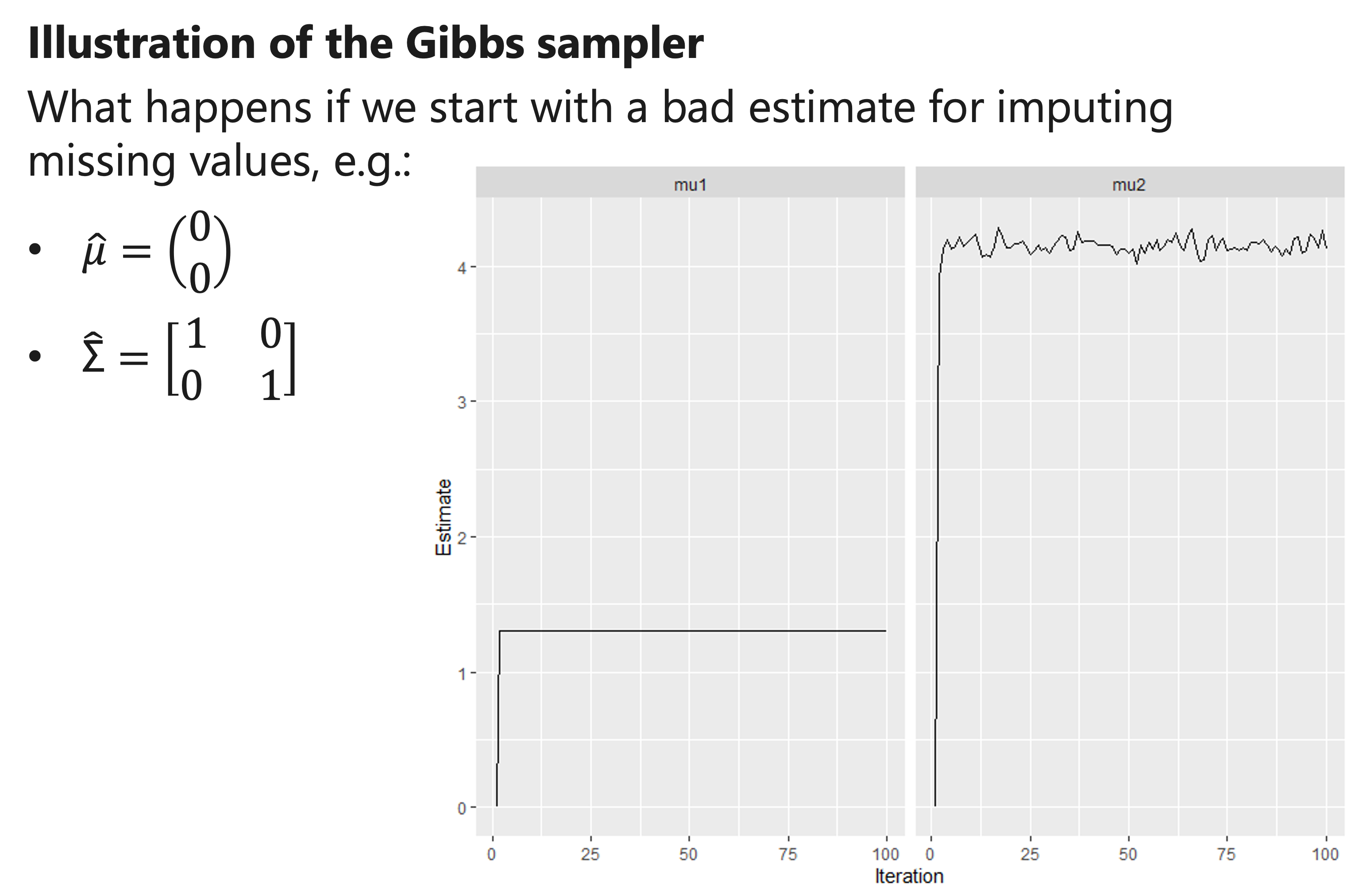
Illustration of the Gibbs sampler
- We impute missing values using the new estimates for μ and “Σ”, and re-estimate μ and “Σ” .
- We iterate this procedure many times.
- Eventually, we should obtain reliable estimates for μ and “Σ” , and thus also obtain imputations that properly reflect their uncertainty
Imputation via Joint Modelling
Imputation via Joint Modelling
How to ensure that we end up in the posterior distribution?
Allow for sufficient imputation cycles!
Repeat the whole process from different starting points
- E.g. Estimate the initial version of μ and Σ in a dataset where all missing values have been replaced by a random value
Imputation via Joint Modelling

Imputation via Joint Modelling

Imputation via Joint Modelling
 ## Imputation via Joint Modelling
## Imputation via Joint Modelling
Imputation via Joint Modelling
Final considerations
Normality assumptions may not always be realistic
- Non-continuous data
- Skewed data
- Nonlinear data
- Clustered data
Several extensions have been proposed to accommodate for this

